梁の反力・曲げﾓｰﾒﾝﾄ・たわみ

ここでは構造力学で使用する静定はりの公式を紹介します。

図　　　　　　形	反力	せん断力	曲げモーメント	たわみ角・たわみ
	RA＝Rb＝P/2	A〜C：Q＝+P/2 C〜B：Q＝-P/2	A〜C：M＝Px/2 C：Mmax＝PL/4	A〜C： y＝PL3 ( 3x / L - 4x3 / L3 ) / 48 E I ymax＝PL3 / 48EI
	RA＝Pb/L RB＝Pa/L	A〜C：Q＝+Pｂ/L C〜B：Q＝-Pa/L	A〜C：M＝Pｂx/L C〜B： M＝Pa(L-x) / L C：Mmax＝Pab/L	A〜C： 　y＝Pa2b2 ( 2x / a + x / b - x3 / a2　　　b ) / 6 E I L 　yc＝Pa2b2 / ( 3 E I L ) a > b の時,　x =0.5773 √( L2 - b2 ) ymax＝Pb √ ( L2 - b2 )3 / ( 9√3 E I L)
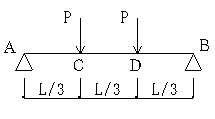
	RA＝RB＝P	A〜C：Q＝+P C〜D：Q＝0 D〜B：Q=-P	A〜C：M=Px C〜D： 　　　Mmax＝PL/3	A〜C： ｙ＝PL3 ( 2x / L - 3x3 / L3 ) / 18 E I C〜D： ｙ＝PL3 ( x / L - x2 / L2 - 1 / 27 ) / 24 E I ymax＝23PL3 / 648 E I
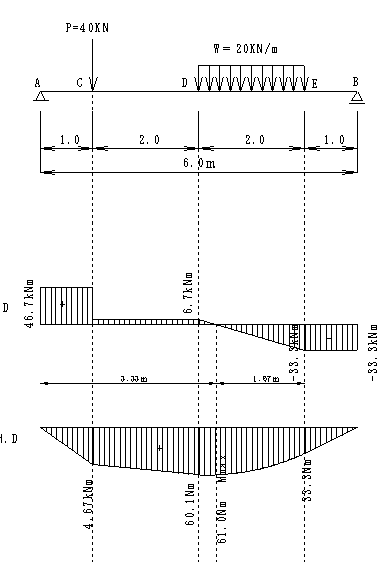
	RA＝RB＝wL/2＝W/2	Q=wL / 2 - wx Qa,b＝ 　　　±　wL / 2	M＝ ( wLx - wx2 ) / 2 Mmax＝wL2 / 8	ｙ＝wL4 ( x / L - 2x3 / L3 + x4 / L4 ) / 24 E I ymax＝5wL4 / 384 E I
	RA＝Wb/L RB＝Wa/L	A〜C’： 　　Q＝Wcb/L C'〜C"： 　　Q＝ wc (( b - a ) / 2L - ( x - a ) / c ) Ｃ”〜Ｂ： 　　Q=- wca / L	A〜C：M=wcbx / L C'〜C"： 　M=wc ( bx / L - ( 2x - 2a + c )2 / 8c 　　　　　　　　　　　) Ｃ”〜Ｂ： 　M=wca ( L - x ) / 　　　　　　　　　　　L x＝a - c / 2 + bc / 　　　　　　　( a + b ) Mmax＝wcab ( a + b ) - c / 2 ) / ( a + b )2	Yc＝wc ( ab ( 2aL - 2a2 - c2 / 4 ) / L 　　　　+ c3 / 64 ) / 6 E I
	RA＝wL / 2 / 3 RB＝2wL / 2 / 3	Q=wL ( 1 - 3x2 　/ L2 ) / 2 / 3 Qa＝+ wL / 2 / 3 Qb＝-2W/3	M=wLx ( 1 - x2 / 　　　　L2 ) / 2 / 3 X=x = L / √3 Mmax＝2wL2 / 2 / 9√3	ｙ＝wL4 ( 7x / L - 10x3 / L3 + 3x5 / L5 ) / 2 / 180 E I ｘ＝0.5193 L ymax＝0.01304wL4 / 2 E L
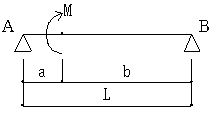
	-	Qa＝- M / L Qb＝- M / L	a > b :aM / L a < b :bM / L	ymax＝M ( L2 - 3b2 )3/2 / 9√3 E I L X=√(( L 2 - 3b2 ) / 3 )
片持梁
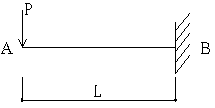
	RB＝P	Q=-P	M=-Px B：Mmax＝-PL	ｙ＝PL3 ( 1 - 3x / 2L + x3 / 2L3 ) / 3 E I A:ymax＝PL3 / 3 E I
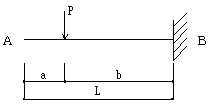
	RB=P	A〜C：Q=0 C〜B：Q=-P	A〜C：M=0 C〜B：M=- P ( 　　　　　x - a ) B：Mmax＝- Pb	C〜B： 　　　ｙ＝Pb3 ( 1 - 3 ( x - a ) / 2b + ( x 　　　　　　　　　　　- a )3 / 2b3 ) / 3 E I ｙｃ＝Pb3 / 3 E I ｙa＝Pb3 ( 1 + 3a / 2b ) / 3 E I
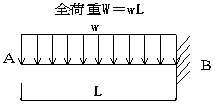
	RB＝ｗL	Q＝-wｘ QB＝-wL	M＝- wx2 / 2 B：Mmax 　　　　＝- wL2 / 2	ｙ＝wL4 ( 1 - 4x / 3L + x4 / 3L4 ) / 8 E I A：ymax＝wL4 / 8 E I
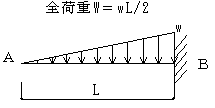
	RB＝wL / 2	Q=- wx2 / 2L QB＝- wL / 2	M=- wx3 / 6L B：Mmax 　　　　＝- wL2 / 6	y＝wL4 ( 1 - 5x /4L + x5 / 4L5 ) / 30 　　　　　　　　　　　　　　　　　　　　　　　E I A：ymax＝wL4 / 30 E I
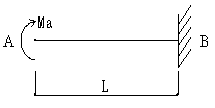
	RB＝0	Q=0	M=Ma M=-Ma	ｙ＝MaL2 ( 1 - x / L )2 / 2 E I A：ymax＝MaL2 / 2 E I
両端固定	-	-	-	-
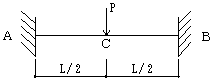
	RA=RB＝P/2	Q=+P/2 Q=-P/2	A〜C： M=PL ( - 1 + 4x / L ) / 8 C〜B： M=PL ( 3 - 4x / L ) / 8 MAB＝-PL / 8 中央：+Mmax 　　　　　　　　　＝PL / 8	ｙ＝PL3 ( x2 / L2 - 4x3 / 3L3 ) / 16 E I 中央：ymax＝PL3 / 192 E I 反曲点：ｙ＝L / 4 , 3L / 4
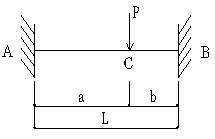
	RA=Pb2 ( 3a + b ) 　　　　　　　　　/ L3 RB=Pa2 ( a + 3b ) 　　　　　　　　　/ L3	A〜C： Q=Pb2 ( 3a + b ) 　　　　　　　　/ L3 C〜B： Q=- Pa2 ( a + 3b 　　　　　　　) / L3	A〜C： M=Pb2 ( - a + ( 3a + b ) x / L ) / L2 C〜B： Pa2 ( a + 2b - ( a + 3b ) x / L ) / L2 MA＝- Pab2 / L2 MB＝- Pa2b / L2 MC=+2Pa2b2 / L3	A〜C： ｙ＝Pb2x2 ( 3a / L - ( 3a + b ) x / L2 ) 　　　　　　　　　　　　　　　　　　　/ 6 E I L C〜B： y=Pb2x2 ( 3a / L - ( 3a + b ) x / L2 ) 　　　　　　　　　　　　　　　　　　　/ 6 E I L ｙｃ＝Pa3b3 / 3 E I L3 a > b の時、x = 2bL / ( 3a + b ) ymax＝2Pa3b2 / ( 3 E I ( 3a + b)2 ) 反曲点：ｘ＝aL / ( 3a + b ) , ( a + 2b ) L / ( a + 3b )
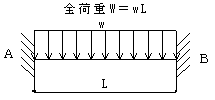
	RA=RB=wL/2＝W/2	Q=±wL / 2	M=wL2 ( - 1 + 6x / L - 6x2 / L2 ) / 12 MA,B＝-wL2 / 12 中央：Mc＝wL2 / 　　　　　　　　　　　　24	ｙ＝wL4 ( x2 / L2 - 2x3 / L3 + x4 / L　　　　　　　　　　　　　　　　　　　　4 ) / 24 E I 中央：Yc＝wL4 / 384 E I 反曲点：X=0.211L , 0.789L
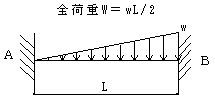
	RA=3wL / 20 RB=7wL / 20	Q=wL ( 3 - 10x2 　　　　/ L2 ) /20	M=wL2 ( - 2 + 9x / L - 10x3 / L3 ) / 60 Ma＝- wL2 / 30 Mb＝- wL2 / 20 x = 0.548L +Mmax＝wL2 / 23.3	y=wL4 ( 2x2 / L2 - 2x3 / L3 + x5 / L　　　　　　　　　　　　　　　　　　　5 ) / 60 E I X=0.525L：ymax＝0.00262wL4 / E I 反曲点：X=0.237L , 0.808L
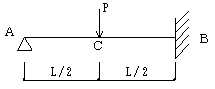
	RA＝5P/16 RB=11P/16	A〜C： Q=5P/16 C〜B： Q=- 11P/16	A〜C：M=5Px/16 C〜B：M=PL ( 1/2 　　　　- 11x/16L ) Mc=5PL / 32 Mb=-3PL/16	A〜C：y=PL3 ( x / L - 5x3 / 3L3 ) / 　　　　　　　　　　　　　　　　　　　　　　32 E I C〜B：y=PL3 ( - 2 / 3 + 5x / L - 8x2 / 　　　　　　　　L2 + 11x3 / 3L3 ) / 32 E I
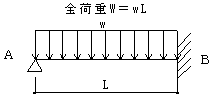
	RA=3wL/8 RB=5wL/8	Q=wL(3/8-x/L )	M=wLx(3-4x/L 　　)/8 MB=-wL2/8 X=3L/8： +Mmax＝9wL2/　　　　　　　　　　　128	y=wL4 ( x / L - 3x3 / L3 + 2x4 / L4 ) / 48 E I X=( 1 + √33 ) L / 16 ： ymax＝wL4 / 184.6 E I 反曲点：X=3L/4
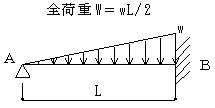
	RA=wL/10 RB=2wL/5 Q=wL ( 1/5-x2/L2 )/2	Q=wL(1/5-x2/L )/2	M=wLx (1/5-x2/3L2)/2 X=L：MB＝- wL2/ 　　　　　　　　　　　15 X=L / √5： +Mmax＝wL2 / 15√5	y=wL4 ( x / L - 2x3 / L3 + x5 / L5 ) / 120 E I X=L / √5： ymax＝2wL4 / 375√5 E I 反曲点：X=√0.6 L