栤戣10偺夝摎
丂丒 俛揰偐傜俙揰偺曽岦妏丂TBA丄嫍棧丂俽BA丂傪媮傔傞丅
丂丂丂丂嚈倃BA丂亖丂XA丂-丂倃俛丂亖丂1526.789丂-丂1732.221 =丂-205.432
丂丂丂丂嚈YBA丂亖丂YA丂-丂YB丂亖丂2514.667丂-丂2454.335丂亖丂60.332
丂丂丂丂倲丂亖丂倲倎値丱-1丂劆嚈倄丂/丂嚈倃劆丂亖丂16亱22乫00乭
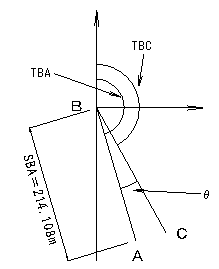
丂丂丂丂t丂偼戞嘦徾尷傛傝丂丂丂TBA丂亖丂163亱38乫00乭
丂丂丂丂SBA丂亖丂併乮嚈倃丱2丂+丂嚈倄丱2乯丂亖丂214.108丂m
丂丒俛揰偐傜俠揰偺曽岦妏丂TBC傪媮傔傞丅
丂丂丂丂嚈倃BC丂亖丂XC丂-丂XB丂亖丂-43.116
丂丂丂丂嚈YBC丂亖丂YC丂-丂YB丂亖丂23.955
丂丂丂t丂亖丂29亱03乫23乭
丂丂丂t丂偼戞嘦徾尷傛傝丂丂丂TBC丂亖丂150亱56乫37乭
丂丂丂兤丂亖丂163亱38乫00乭丂-丂150亱56乫37乭丂亖丂12亱41乫23乭
丂丂恾偺傛偆偵俛揰偵僩儔儞僔僢僩傪悩偊偰丄俠揰傪婎弨乮0僙僢僩乯偵
丂丂丂
丂丂丂兤丂亖丂12亱41乫23乭丂偺妏傪怳傝丄偦偺帇弨慄忋偵俛揰傛傝
丂丂丂SBA丂亖丂214.108丂m丂偺嫍棧傪偲傞偲俙揰傪應愝偱偒傞丅

丂丂丂丂丂