測量練習問題
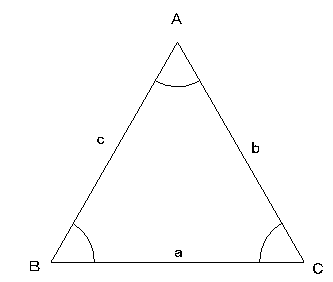
§三角形の性質について
正弦定理 a / sin A = b / sin B = c / sin C
余弦定理 a^2 = b^2 + c^2 - 2 * b * c * cosA
問題 1 C.L.=20m 、R=3000m の時の弦長ABを求めよ。
問題 2 C.L.=20m 、R=300m の時の弦長ABを求めよ。
§単曲線について
TL = R * tan ( I / 2 )
AB = 2 * R * sin ( I / 2 )
M = R * { 1 - cos ( I / 2 )}
SL = R * { sec ( I / 2 ) - 1 }
CL = R * π / 180°* I°
I°/ 2 = ( CL / R ) * ( 180°/ 2π )
・逆数関係 cot θ= 1 / tan θ
sec θ= 1 / cos θ
cosec θ= 1 / sin θ
・相除関係 tan θ = sin θ / cos θ
cot θ = cos θ / sin θ
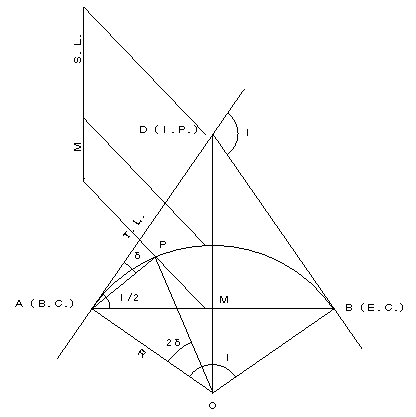
問題 3 I=82°43’27”、 SL=12m の時、Rはいくらか?
問題 4 トランシットによる測角法を2つ挙げよ。
問題 5 水平距離の測量方法を2通り挙げよ。
問題 6 弦角弦長法
σ=1718.873 * L / R を用いて次の測角を求めなさい。
R = 6500m
| 測点 | 単距離 | 追加距離 | σ | 360°-σ |
| NO.1(BC) | 0 | 0 | 0 | 0 |
| NO.2 | 0.786 | 0.786 | A | B |
| NO.3 | 20 | 20.786 | C | D |
| NO.4 | 20 | 40.786 | E | F |
| NO.5 | 20 | 60.786 | G | H |
| NO.6(EC) | 184.309 | I | J |
§三角高低測量
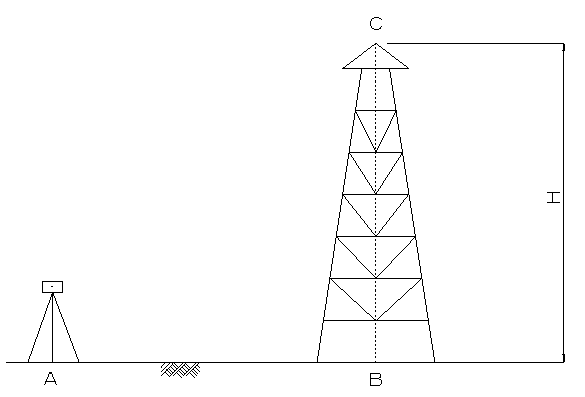
問題 7 下図の送電線の高さ H を求めるには、どうしたら良いか?使用できる道具は、トランシット、テープ、スタッフです。
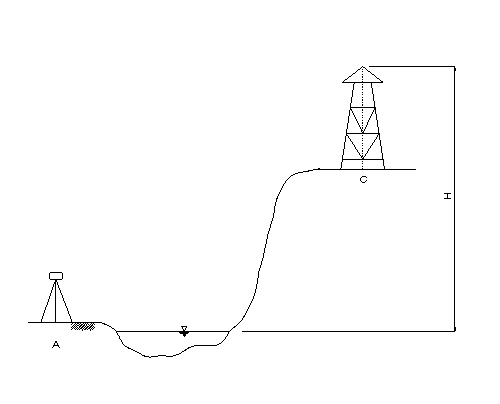
問題 8 下図の送電線の頂点から河川の水面までの高低差 Hを測りなさい。使用道具は、トランシット、テープ、スタッフです。
§座標について
問題 9 次の2点の既知点間の方向角と距離を算出しなさい。
NO.1 X1=521176.9310 Y1=-21321.6140
NO.2 X2=521179.6528 Y2=-21309.7143
問題 10 次のA、B、Cの3つの既知点座標を使い、B、C点は現地にあるものとして、この2点を利用してA点を現地に落とす方法を述べよ。
A ( 1526.789 、 2514.667 ) B ( 1732.221 、 2454.335 ) C ( 1689.105 、 2478.290 )
問題 11 次の測点 P の座標値を求めなさい。
方向角 315°49’22”
測点A (X1 = -157473.1984 、 Y1 = -39329.2981 )
測角 θ = 268°01’ 03” 測距 I = 181.993
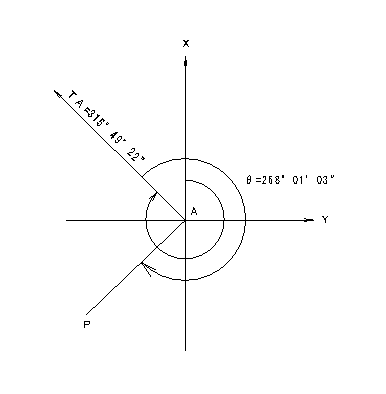
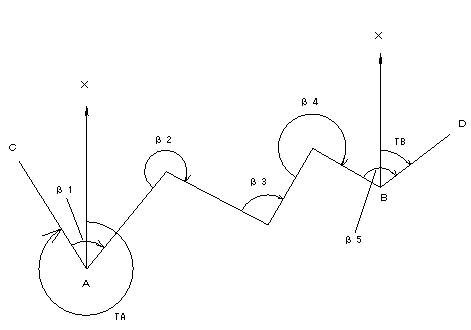
問題 12 図のような三角点A〜B間の結合トラバースを行い、次の観測値を得た。
β1 = 80°20’32”
β2 = 260°55’18”
β3 = 91°34’20”
β4 = 260°45’44”
β5 = 110°05’42”
既知点間の方向角を
TA = 330°14’20”
TB = 53°56’28”
としたとき、観測方向角の閉合差はいくらか?
§水準測量
問題 13 以下の水準測量を行ったものとし、野帳の中を埋めなさい。
| 測点 | BS | IH | FS | GH | PH | 差 |
| 仮BM | 1.245 | 52.145 | ||||
| A | ||||||
| NO.1 | 2.143 | B | ||||
| NO.2 | 1.864 | C | ||||
| TP1 | 1.045 | D | ||||
| 1.478 | ||||||
| E | ||||||
| NO.3 | 2.105 | F | ||||
| TP2 | 1.779 | G | ||||
| 1.328 | ||||||
| H | ||||||
| NO.4 | 1.069 | I |